| Språk : |
|
| Encyclopedia gemenskap |Encyclopedia Svar |Submit fråga |Ordförråd Kunskap |Överför kunskap |
Naturlig logaritm |
 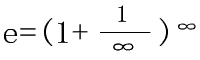 |
|
Antalet e är lim (1 1 / x) ^ x, x-> ∞ eller lim (1 z) ^ (1 / z), z-> 0, värde ca 2,71828, är inte en oändlig antal cykler. Ursprung Spiralformade eller spiral linje är mycket vanlig naturlig form av existensen av saker, till exempel: en WISP av rök krypa upp på en blå himmel, gled en Avon försiktigt skvalpar, några endast långsamt klättra stängslet och många sniglar I lugn och ro den stjärnklara natthimlen för att få kramade virvlar ......Spiral logaritmisk spiral särskild estetisk betydelse indexet kan uttryckas i formen: [1] Där är α och k en konstant, φ är den polära vinkeln är ρ polarradien, e är naturliga logaritmen. För att underlätta diskussionen, är vi e eller e efter en viss förening i form av förvandling och definieras som "naturliga lagen." Därför är "naturlagarna" är kärnan i e. e, som en matematisk konstant är en funktion av den naturliga logaritmen basen. Ibland kallas Eulers nummer (Euler nummer), uppkallad efter den schweiziske matematikern Leonhard Euler, också har en relativt ovanlig namn Napier konstant, för att fira minnet av den skotska matematikern John Napier introduktion logaritmen?. Det är som pi π och den imaginära enheten i, är e de viktigaste matematiska konstanter. Dess värde är omkring (decimal 100): "e ≈ 2,71828 18284 59045 23536 02874 71352 66249 77572 47093 69995 95749 66967 62772 40766 30353 54759 45713 82178 52516 64274" Det första omnämnandet av konstanten e, var John Napier (John Napier) 1618, publicerat flera böcker på ett bord i appendix. Men det visar inte konstant bara av dess botten beräknas som en naturlig logaritm av listan, brukar anses vara av William Oughtred (William Oughtred) produktion. E för att se den första gången som en konstant, Jacob Bernoulli (Jacob Bernoulli). Den första kända användningen konstant e är Leibniz år 1690 och 1691 till Huygens kommunikationer till B representerar. 1727 inleddes med Euler konstant e att ange detta, medan e först används i publikationen är 1736 Eulers "mekanik" (Mechanica). Även senare forskare sade också att med bokstaven c, e, men mer vanligt, och slutligen blivit standard. Genom e representerar den exakta orsaken är okänd, men förmodligen eftersom e är "index" (exponentiell) den första bokstaven i ordet. En annan uppfattning som kallas a, b, c, och d är andra återkommande syften och e är den första tillgängliga bokstaven. Dock är orsaken till brevet Euler valet osannolikt eftersom detta är hans första bokstaven i hans namn Euler, eftersom han är en mycket ödmjuk person, alltid korrekt bekräftade andras arbete. Många tillväxt eller processer sönderfallsprodukter kan simuleras med den exponentiella funktionen. Viktig aspekt av den exponentiella funktionen är att det är den enda funktionen och dess derivat är lika (multipliceras med en konstant). e är irrationellt och transcendentalt numrerar (se Lindemann - 魏尔施特拉斯 Sats (Lindemann-Weierstrass)). Detta är den första certifierad som en transcendental antal, snarare än medvetet konstruerat (jämför Liouville nummer), av Charles Hermite (Charles Hermite) år 1873 visade. Kort introduktion Bortom främst bara naturliga konstanter (e) och pi (π). Naturligt konstant synlighet är mycket mindre än omkretsen eftersom pi lättare att stöta på i verkliga livet, medan naturkonstanterna inte används ofta i vardagen. Integration av e, π den mest perfekta Eulers formel e ^ (iπ) 1 = 0, är också ett transcendentalt numrerar e det högsta uttrycket för det matematiska värdet. Konstanter i naturen är i allmänhet en makt bas formel och logaritmer. Varför är det, beroende på dess ursprung. Till Frankrike än den naturliga konstanten pi är mycket enklare. Det är funktionen y = f (x) = (1 1 / x) ^ x, när x går mot oändligheten y gränser. Samtidigt är det också lika med 1/0! 1/1! 1/2! 1/3! 1/4! 1/5! ....... Visar också 0! Är lika med 1. Naturliga konstanter i formler gör ofta logaritmer. Till exempel, för den exponentiella och logaritmiska funktioner härledning, är det nödvändigt att använda naturliga konstant. Funktionen y = f (x) = a ^ x av derivatet f '(x) = a ^ x * ln (a). Funktionen y = f (x) = loga (x) är derivatan f '(x) = loga (e) / x. Naturliga konstanter samt primtal distribution. Det är ett naturligt tal en, då den är mindre än primtal ensam om en / ln (a) en. I en liten, är resultatet inte är korrekt. Men som ett ökar kommer detta teorem att vara mer exakt. Denna sats kallas primtalssatsen, Gauss upptäckt. Dessutom finns det andra användbara konstanter av naturen. Som problemlösning. Vänligen skicka 100 uppdelad i flera delar, så att produkten av varje så stor som möjligt. För att analysera innebörden av frågorna, är att summan av två tal a och b, så ab = 100, som söker en b-e max. (Beskrivning, kan en vara varje rationellt tal, måste b vara ett heltal.) På denna punkt måste du använda naturliga konstant. Det måste vara så nära ett e. Då b bör vara 100 / e ≈ 36,788 exemplar, men på grund av det antal kopior som ska vara ett heltal, så tar de ungefärliga 37 exemplar. På detta sätt var och en av 100/37, så att det maximala värdet för en b-te potensen av ungefär "94.740.617 167.818 32,652." e är ett transcendent tal är mycket vanligt en, är det vanligtvis används som en naturlig logaritm. e beräkningsmetod Använd Windows kalkylator: menu "Visa / Science-typ", och sedan följt genom att klicka på en hyp synd (1 hyp cos 1) eller med tangentbordet 1HS (1HO) = eller (1HS (1HO)) är också tillgänglig härifrån med Ctrl C kopierar, sedan byta till räknaren, tryck ctrl V (menyn "Redigera / Klistra in"), får sina 32 värden: "E = 2,71828 18284 59045 23536 02874 71352 6" (nr 31 decimaler avrundas till 7) e ingen rationell bevis för transcendens Klicka för att förstora Naturligt konstant e irrationella transcendentala bevis e decimal 2000 Detta ligger bakom decimaltecknet två tusen: |
| Användare Omdöme |
|
Inga kommentarer |